Издательство «Манн, Иванов и Фербер» представляет книгу профессора математики Джордана Элленберга «Форма реальности. Скрытая геометрия стратегии, информации, общества, биологии и всего остального» (перевод Евгения Поникарова).
Математику называют царицей наук, а ее часть — геометрия — лежит в основе понимания мира. Профессор математики в Висконсинском университете в Мэдисоне, научный сотрудник Американского математического общества Джордан Элленберг больше 15 лет популяризирует свою любимую дисциплину.
В этой книге с присущими ему легкостью и юмором он рассказывает, что геометрия не просто измеряет мир — она объясняет его. Она не где-то там, вне пространства и времени, а здесь и сейчас, с нами. Она помогает видеть и понимать скрытые взаимосвязи и алгоритмы во всем: в обществе, политике и бизнесе. Геометрия скрывается за самыми важными научными, политическими и философскими проблемами.
Предлагаем прочитать одну из глав книги.
Три года воскресений
Действительно важный и в каком-то смысле замалчиваемый факт о математике — она очень сложна. Иногда мы скрываем этот факт от учеников, полагая, что оказываем им услугу. Как раз наоборот. Будучи стажером у преподавателя Робина Уильямса, я научился у него одной простой вещи. Когда мы говорим, что этот урок легкий или простой, а это явно не так, мы даем учащимся понять, что проблемы не в математике, а в них. И они нам верят. К худу или к добру, но ученики доверяют учителям. «Если я не понял даже то, что было просто, — скажут они, — то зачем вообще утруждать себя попытками понять что-то сложное?»
Наши ученики боятся задавать вопросы в классе из-за опасений «выглядеть глупо». Если бы мы честно признались, насколько трудна и глубока математика, то даже та математика, которую изучают на уроках геометрии в старших классах, явно стала бы меньшей проблемой: мы оказались бы в классах, где задавать вопросы значило бы не «выглядеть глупо», а наоборот — «выглядеть как человек, который хочет чему-то научиться». И это относится не только к слабым ученикам. Да, некоторые легко усваивают основные правила алгебраических операций или геометрических построений, но даже им следует задавать вопросы — учителям и себе. Например: я сделал то, что просил учитель, но что, если бы я попробовал сделать что-то другое, о чем учитель не спрашивал? И кстати, почему учитель просил то, а не иное? Нет такой интеллектуальной вершины, с которой вы не сможете увидеть какой-то пробел в знаниях, и именно туда и нужно направить усилия, если вы хотите учиться. Если урок математики легкий, значит, вы что-то делаете неправильно.
Что такое вообще сложность? Это одно из тех слов, которые, как нам кажется, мы хорошо знаем, но при попытках их описать они распадаются на связанные, но разные понятия. Мне нравится история, рассказанная специалистом по теории чисел Эндрю Грэнвиллом об алгебраисте Фрэнке Нельсоне Коуле1.
На заседании Американского математического общества в 1903 году Коул подошел к доске и, не говоря ни слова, вычислил величину 267 – 1 = 147 573 952 589 676 412 927. Затем на второй части доски он написал 193 707 721 × 761 838 257 287, перемножил эти числа и получил то же самое число. После этого он, по-прежнему не сказав ни слова, сел на свое место, а впоследствии признался, что разложение числа 267 – 1 на два множителя заняло у него «три года воскресений». Мораль этой истории в том, что, хотя Коулу потребовались огромные усилия и настойчивость, чтобы найти эти множители, ему не понадобилось много времени, чтобы продемонстрировать и обосновать свой результат в аудитории математиков (и доказать свою правоту). Таким образом, как мы видим, доказательство может быть коротким, даже если его поиск занял массу времени.
Одно дело — трудность в признании истинности какого-нибудь утверждения, и совсем другое — трудность в придумывании утверждения, истинность которого должна быть признана. Именно этому достижению аплодировала аудитория Коула. Мы уже видели, что поиск простых делителей для больших чисел — это сложная задача; однако число 147 573 952 589 676 412 927 по стандартам современной компьютерной техники вовсе не является большим. Я только что разложил его на своем ноутбуке, и это заняло не целое воскресенье, а совершенно незаметный промежуток времени. Так сложна эта задача или нет?
Или рассмотрим проблему вычисления цифр числа π; когда-то это занятие считалось исследовательской математикой, но сейчас это всего лишь простые расчеты. Здесь появляется еще один вид трудности — трудность мотивации. Я не сомневаюсь, что моих технических умений вычислять хватит, чтобы вручную найти семь или восемь цифр π. Но мне было бы очень непросто заставить себя это сделать, потому что это скучно, потому что за меня это может сделать мой компьютер и (возможно, самое главное) потому что нет причин знать очень много цифр этого числа. Конечно, существуют ситуации, где понадобится семь-восемь цифр. Но сотая цифра? Сорока цифр уже вполне достаточно, чтобы вычислить длину окружности размером с нашу Галактику с точностью до размера протона.
Знать сто цифр числа π — вовсе не значит знать о кругах больше, чем другие люди. В числе π важно не его значение, а то, что оно само имеет большое значение. Значимым фактом будет то, что отношение длины окружности к ее диаметру не зависит от ее размера и местоположения. Это факт о симметрии плоскости. Любую окружность можно преобразовать в другую с помощью так называемого подобия, состоящего из переносов, вращений и изменений масштаба. Подобие может менять расстояния, однако делает это путем умножения на фиксированную константу: возможно, все расстояния удваиваются, возможно, уменьшаются в десять раз, но в любом случае отношение между двумя длинами (скажем, длиной окружности и длиной ее диаметра) остается тем же. Если вы считаете две фигуры одинаковыми, когда их можно перевести друг в друга путем симметрий такого рода (называя разные вещи одним именем в стиле Пуанкаре), то в реальности существует всего одна окружность, а потому и только одно число π. Аналогично есть только один квадрат и, соответственно, только один ответ на вопрос «Каково отношение периметра квадрата к его диагонали?»2, и этот ответ равен удвоенному квадратному корню из 2, то есть примерно 2,828… и эту величину можно назвать числом π для квадрата. Точно так же есть только один правильный шестиугольник, и его π равно 3.
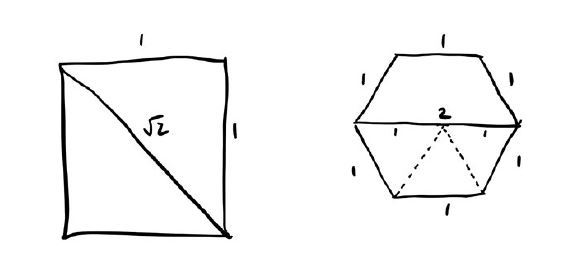
А вот у прямоугольника числа π нет, потому что существует не один прямоугольник, а много, отличающихся отношением между длинной и короткой сторонами.
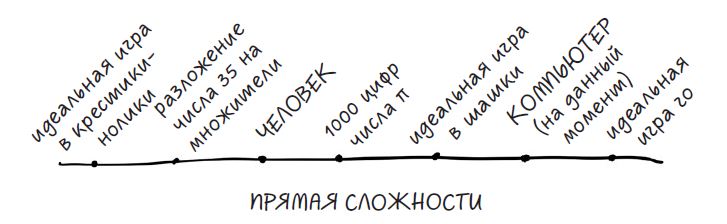
Сложно ли сыграть идеальную партию в шашки? Для человека — да, но компьютерной программе «Чинук» вполне по силам. (Правильно ли ставить вопрос не о сложности, с которой сталкивается «Чинук» в игре, а о сложности, с которой столкнулись ученые при создании программы?) Как мы видели, задача игры в идеальные шашки, идеальные шахматы или идеальное го принципиально ничем не отличается от перемножения двух больших чисел. А разве в каком-то смысле это действие не концептуально простое? Мы точно знаем, что нужно сделать, чтобы проанализировать дерево игры, даже если в реальности нам не хватит на это времени жизни Вселенной.
Один простой ответ — сказать, что некоторые задачи, такие как разложение чисел на множители или игра го, просты для компьютеров и сложны для нас, потому что компьютеры лучше и умнее нас. Такой ответ неявно моделирует сложность в виде некоторой точки на прямой, где также можно расположить людей и компьютеры, при этом их положение определяется умением решать все задачи, размещенные левее.
Однако это неверно: геометрия сложности не одномерна. Существуют задачи — например, разложение больших чисел на множители, идеальная игра в шашки или хранение миллиардов слов с идеальной точностью, — с которыми компьютеры справляются гораздо, гораздо лучше нас. (Прежде всего, компьютеры не сталкиваются с проблемой мотивации: они делают — во всяком случае, на данный момент — то, что мы им говорим.) Но есть задачи, сложные для компьютеров и легкие для нас. Известный пример — проблема четности: стандартные архитектуры нейронных сетей очень плохо с ней справляются. Скажем, в строке из букв X и O четное или нечетное количество букв X? Трудности возникают и с экстраполяцией. Если вы приведете человеку кучу подобных примеров:
вход: 2,2 выход: 2,2
вход: 2,4 выход: 2,4
вход: 1,0 выход: 1,0
вход: 4,1 выход: 4,1
вход: 5,0 выход: 5,0
и спросите, что будет на выходе, если на входе 3,2, то он скажет: 3,2. То же самое выдаст и нейронная сеть, обученная на этих данных. А если на входе будет 10,0? Человек скажет 10,0. А вот нейронная сеть может ответить что угодно. Существует масса безумных правил, которые согласуются с формулой «вход = выход» в промежутке от 1 до 5, но ведут себя совершенно иначе вне этого диапазона. Человек знает, что «вход = выход» — это самый простой и естественный способ экстраполировать правило на более широкий класс возможных входных сигналов, а вот алгоритм машинного обучения не знает. Вычислительные мощности у него есть, а понимания нет.
Естественно, я не могу исключить, что машины со временем (или даже неизбежно!) превзойдут когнитивные способности людей во всех аспектах. Такую вероятность исследователи искусственного интеллекта признавали всегда. Один из пионеров в этой области Оливер Селфридж в телевизионном интервью начала 1960-х годов сказал: «Я убежден, что машины могут и будут думать при нашей жизни», хотя и с оговоркой: «Не думаю, что моя дочь когда-либо выйдет замуж за компьютер». (Нет настолько абстрактных технических достижений, чтобы люди не ощущали сексуального беспокойства по этому поводу.) Многомерная геометрия сложности должна нам напоминать, что очень трудно понять, какие умения машины находятся на грани появления. Возможно, автомобиль без водителя делает правильный выбор в 95 % случаев; но как раз приходящиеся на оставшиеся 5 % исключительные случаи и могут быть той самой проблемой, для решения которой наши тестообразные мозги приспособлены лучше, чем любая современная или разработанная в ближайшем будущем машина.
И конечно же, меня по понятным причинам интересует вопрос, может ли машинное обучение заменить математиков. Не берусь предсказывать, но надеюсь, что математики и машины останутся партнерами, как и сейчас. Многие вычисления, отнимавшие у математиков годы воскресений, сегодня можно делегировать нашим механическим коллегам, что позволит нам заниматься тем, в чем мы особенно хороши.
Пару лет назад Лиза Пиччирилло, в то время аспирантка в Техасском университете, решила давнюю геометрическую задачу об узле Конвея, доказав, что это не срезанный узел (это факт о том, как выглядит узел с точки зрения четырехмерных существ, но для нашей истории не имеет значения, что это в точности означает). Это была знаменитая сложная задача. Но даже здесь значение слова непонятно: задача была сложной, потому что многие математики безуспешно работали над ней, или легкой, потому что Пиччирилло нашла элегантное решение всего на девяти страницах, из которых две — рисунки? Один из моих наиболее часто цитируемых результатов обладает той же природой: шестистраничная статья решает проблему, над которой я и многие другие математики трудились в течение двадцати лет. Может быть, нам нужно новое слово, которое означало бы не «это легко» или «это сложно», а «сложно осознать, что это легко»?
За несколько лет до Пиччирилло тополог по имени Марк Хьюз из Университета Бригама Янга пытался создать нейронную сеть, которая позволяла бы узнать, какие узлы срезаны. Он предоставил ей длинный список узлов, для которых ответ был известен, — точно так же, как нейронная сеть, обрабатывающая изображения, получала длинный список изображений кошек и некошек. Нейронная сеть Хьюза научилась присваивать каждому узлу определенное число: если узел был срезанным, то число должно быть 0, если не срезанным, то предполагалось, что машина должна выдавать целое число больше 0. На деле нейронная сеть спрогнозировала значение, очень близкое к 1 (то есть предсказала, что узел не срезанный), для всех узлов, протестированных Хьюзом, — за исключением одного. Это был узел Конвея. Нейронная сеть выдала число, весьма близкое к 1/2: это ее способ сказать, что она совершенно не уверена, какой должен быть ответ — 0 или 1. Потрясающе! Нейронная сеть правильно определила узел, действительно представляющий трудную и математически богатую проблему (в данном случае она воспроизвела то интуитивное представление, к которому топологи уже давно пришли). Некоторые люди воображают мир, где компьютеры дают нам все ответы. Я мечтаю о большем. Я хочу, чтобы они задавали хорошие вопросы.
1. Согласно Мартину Гарднеру, это история из книги Эрика Темриля Белла «Математика — царица и служанка науки». См. Гарднер М. Математические досуги. М.: Мир, 1972, с. 419. — Прим. науч. ред.
2. Почему к диагонали? Я считаю ее хорошим аналогом диаметра, потому что это самое большое расстояние между точками фигуры.