Издательство «Манн, Иванов и Фербер» представляет книгу ученого и популяризатора науки Сергея Самойленко «Вероятности и неприятности. Математика повседневной жизни».
«Законы подлости» существуют! Книга познакомит вас с ними и покажет, что они математически красивы. А кроме того, из них можно извлечь пользу в самых разных житейских ситуациях, где существует неопределенность и многовариантность.
Может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе? Правда ли, что дожди чаще идут в выходные? Отчего большая часть дел всегда остается на последнюю ночь? Почему «на вкус и цвет товарищей нет», а автобуса почти всегда приходится ждать долго? Пришло время узнать, как работают «законы подлости» — от закона арбузной корки («покупая многомерный арбуз, ты приобретаешь в основном его корку») до наблюдения Этторе («соседняя очередь всегда движется быстрее»).
Несовершенство нашего мира и жизненные закономерности имеют объективное математическое обоснование. С помощью жизненных примеров автор познакомит вас с миром нешкольной математики: теорией вероятностей и математической статистикой, а также смежными областями — теорией мер, марковских цепей, стохастических процессов, очередей, динамического хаоса.
Предлагаем прочитать один из разделов книги.
Статистика как научный способ чего-либо не знать
Цифры обманчивы, особенно когда я сам ими занимаюсь; по этому поводу справедливо высказывание, приписываемое Дизраэли: «Существует три вида лжи: ложь, наглая ложь и статистика».
Марк Твен1
Как часто летом мы намереваемся на выходные выехать на природу, прогуляться в парке или устроить пикник, а потом дождь разбивает наши планы, заточив нас в доме! И ладно бы это случалось раз или два за сезон; порой складывается впечатление, что непогода преследует именно выходные дни, раз за разом выпадая на субботу или воскресенье!
Совсем недавно вышла статья австралийских исследователей «Недельные циклы пиковой температуры и интенсивность городских тепловых островов»2. Ее подхватили новостные издания и перепечатали результаты с таким заголовком: «Вам не кажется! Ученые выяснили: погода на выходных действительно хуже, чем в будние дни». В цитируемой работе приводится статистика температуры и осадков за много лет в нескольких городах Австралии, и вправду выявляющая понижение температуры на 0,3 °C в определенные часы субботы и воскресенья. Там же этому дается объяснение. Оно связывает локальную погоду с уровнем загрязненности воздуха из-за возрастающего транспортного потока. Незадолго до того подобное исследование проводилось в Германии3 и привело примерно к тем же выводам.
Согласитесь, доли градуса — весьма тонкий эффект. Сетуя на непогоду в долгожданную субботу, мы обсуждаем, был ли день солнечным или дождливым. Такое обстоятельство проще зафиксировать, а позже вспомнить, даже не обладая точными приборами. Мы проведем собственное небольшое исследование на эту тему и получим замечательный результат: можно уверенно утверждать, что мы не знаем, связаны ли на Камчатке день недели и непогода. Исследования с отрицательным результатом обычно не попадают на страницы журналов и в новостные ленты, но нам важно понять, на каком основании мы можем что-либо уверенно заявлять о случайных явлениях. И в этом плане отрицательный результат ничем не хуже положительного.
Слово в защиту статистики
Статистику обвиняют во множестве грехов: и во лжи, и в возможностях манипуляций, и, наконец, в непонятности. Но мне очень хочется реабилитировать эту область знаний, показать, насколько сложна задача, для которой она предназначена, и как непросто понять ответ, который дает статистика.
Теория вероятностей оперирует точными знаниями о случайных величинах в виде распределений или исчерпывающих комбинаторных подсчетов. Еще раз подчеркну, что иметь точное знание о случайной величине возможно, если мы говорим о распределении. Но что если это знание нам недоступно, а единственное, чем мы располагаем, — наблюдения? У разработчика нового лекарства есть ограниченное число испытаний, у создателя системы управления транспортным потоком — лишь ряд измерений на реальной дороге, у социолога — результаты опросов. Причем он может быть уверен в том, что, отвечая на какие-то вопросы, респонденты просто соврали.
Понятно, что одно наблюдение не дает ровным счетом ничего. Два — немногим больше. Сколько нужно наблюдений — три, четыре, сто, — чтобы получить какое-то знание о случайной величине, в котором можно быть уверенным в математическом смысле? И что это за знание? Скорее всего, оно будет представлено в виде таблицы или гистограммы, дающей возможность оценить некоторые параметры случайной величины, например область определения, среднее или дисперсия, асимметричность и т. д. Быть может, глядя на гистограмму, удастся угадать точную форму распределения. Это и есть основная задача математической статистики: по наблюдаемым реализациям случайной величины выяснить ее распределение, то есть получить по возможности точное и исчерпывающее ее описание. Но — внимание! — все результаты наблюдений сами будут случайными величинами! Пока мы не владеем точным знанием о распределении, все результаты наблюдений дают нам лишь вероятностное описание случайного процесса! Случайное описание случайного процесса — еще бы здесь не запутаться, а то и захотеть запутать намеренно!
Что же делает математическую статистику точной наукой? Ее методы позволяют заключить наше незнание в четкие рамки и дать вычислимую меру уверенности в том, что в этих рамках наше знание о случайной величине согласуется с фактами. Это язык, на котором можно говорить о случайностях неизвестной природы так, чтобы рассуждения имели смысл. Такой подход очень полезен в философии, психологии и социологии, где очень легко пуститься в пространные рассуждения и дискуссии без надежды на получение настоящего знания и тем более доказательства. Грамотной статистической обработке данных посвящено множество книг, ведь это абсолютно необходимый инструмент для медиков, социологов, экономистов, физиков, психологов — словом, всех специалистов, научно исследующих «реальный мир», который отличается от идеального математического лишь степенью нашего незнания о нем. Я получил упрек за то, что использовал кавычки вокруг слов «реальный мир», как если бы не верил в его существование. Такое направление в философии действительно есть, оно называется солипсизмом, но я не его сторонник. Кавычками я хочу подчеркнуть, что не разделяю мир на реальный и идеальный, физический и математический. Я не вижу причин считать математические структуры тем, чего нет в мире, в котором мы живем. Это глубокий вопрос и давний спор: математик исследует настоящую вселенную или изобретает свою, ненастоящую? Я не хочу долго рассуждать на эту тему, поскольку не вижу, как тот или иной ответ может помочь математику или физику в его работе. Но одним из чудес нашего мира по праву считается то, что он описывается на языке математики, доступном человеку.
Теперь еще раз взгляните на эпиграф к этой главе и осознайте, что статистика, которую так пренебрежительно называют третьим видом лжи, — единственное, чем располагают все естественные науки. Это ли не главный закон подлости мироздания! Все физические и наблюдаемые нами экономические законы строятся на математических моделях и их свойствах, но проверяются они статистическими методами в ходе измерений и наблюдений. В повседневности наш разум делает обобщения и подмечает закономерности, выделяет и распознает повторяющиеся образы. Это, наверное, лучшее, что умеет человеческий мозг. Именно этому в наши дни учат искусственный интеллект. Но разум экономит силы и склонен делать выводы по единичным наблюдениям, не сильно беспокоясь о точности или обоснованности этих заключений. По этому поводу есть замечательное самосогласованное утверждение из книги Стивена Браста «Исола»4: «Все делают общие выводы из одного примера. По крайней мере, я делаю именно так». И пока речь идет об искусстве, характере домашних любимцев или обсуждении политики, об этом можно сильно не беспокоиться, однако при строительстве самолета, организации диспетчерской службы аэропорта или тестировании нового лекарства уже нельзя сослаться на то, что «мне так кажется», «интуиция подсказывает» и «в жизни всякое бывает». Тут приходится ограничивать работу своего разума рамками строгих математических методов.
Эта книга — не учебник, мы не будем детально исследовать статистические методы и ограничимся лишь одной из техник проверки гипотез. Но мне хотелось бы показать ход рассуждений и форму результатов, характерных для этой области знания. И, возможно, кому-то из читателей, будущему студенту, не только станет понятно, зачем его мучат матстатистикой, всеми этими QQ-диаграммами, t- и F-распределениями, но и придет в голову другой важный вопрос: а как вообще возможно знать что-нибудь наверняка о случайном явлении? И что именно мы узнаём, используя статистические данные?
Как возможность ошибиться делает науку наукой
Математическая статистика использует методы теории вероятностей, а ее столпы — закон больших чисел и центральная предельная теорема.
Естественное предположение, что наблюдаемые данные отражают реальное неизвестное распределение, оказывается верным. Например, гистограмма наблюдаемых величин приближается к истинной плотности распределения, если число наблюдений стремится к бесконечности.
Как закон больших чисел, так и центральная предельная теорема — не одно утверждение. Каждый из этих результатов представляет собой несколько разных теорем, охватывающих широкий спектр задач и условий. Мы познакомимся с их упрощенными формулировками, дающими хорошее представление об этих важных результатах.
Закон больших чисел — несколько разных теорем, утверждающих, что среднее значение наблюдений случайной величины при определенных условиях в том или ином смысле стремится к неизвестному математическому ожиданию этой величины. В простейшем случае он выглядит так. Пусть X1,X2,…,Xn — независимые одинаково распределенные случайные величины с математическим ожиданием a, Sn = X1 + X2 +…+ Xn. Тогда
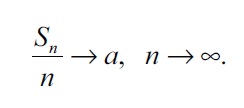
Иными словами, среднее значение наблюдений стремится к математическому ожиданию. В частности, из закона больших чисел вытекает, что частота наблюдений какого-либо события стремится к вероятности этого события, то есть он прочно связывает «бытовое» частотное толкование вероятности и теоретическое как меры на вероятностном пространстве.
Центральная предельная теорема говорит о том, что при определенных условиях сумма независимых или слабо зависимых случайных величин, каждая из которых вносит небольшой вклад в общую сумму, имеет распределение, близкое к нормальному (гауссовскому). Теорема получила свое название за универсальность и важность, поскольку ее условия часто реализуются на практике. Например, многие биологические характеристики (рост человека или размах рук) подчиняются нормальному распределению, поскольку на них влияет множество факторов (скажем, действует много разных генов), вносящих по отдельности небольшой вклад. В простейшем случае теорема выглядит так.
Пусть опять X1,X2,…,Xn — независимые одинаково распределенные случайные величины с математическим ожиданием a и дисперсией σ2. Тогда

Здесь N(0,1) обозначает стандартное нормальное распределение со средним 0 и дисперсией 1.
Иными словами, при больших n сумма Sn близка к гауссовской случайной величине с математическим ожиданием (средним значением) na и дисперсией nσ2.
Эту теорему обычно доказывают, применяя методы функционального анализа. Но мы увидим позже, что ее можно понять и даже расширить, введя понятие энтропии как меры вероятности состояния системы: нормальное распределение имеет наибольшую энтропию при наименьшем числе ограничений. В этом смысле оно оптимально при описании неизвестной случайной величины либо случайной величины, являющейся суммой многих других величин, распределение которых тоже неизвестно.
Эти два закона лежат в основе количественных оценок достоверности наших знаний, основанных на наблюдениях. Здесь речь о статистическом подтверждении или опровержении предположения, которое можно сделать из каких-то общих оснований, и математической модели. Это может показаться странным, но сама по себе статистика не производит новых знаний. Набор фактов превращается в знание лишь после построения связей между фактами, образующих определенную структуру. Именно эти структуры и связи позволяют делать предсказания и выдвигать общие предположения, которые основаны на чём-то, выходящем за пределы статистики. Они называются гипотезами. Самое время вспомнить один из законов мерфологии — постулат Персига:
Число разумных гипотез, объясняющих любое данное явление, бесконечно.
Задача математической статистики — ограничить это бесконечное число, а вернее, свести все гипотезы к одной, причем вовсе не обязательно верной. Итак, у нас есть случайная величина X, распределение P которой неизвестно (иногда совсем, иногда частично). Гипотеза — любое предположение о P. Простая гипотеза — предположение, что P — какое-то конкретное известное распределение. Сложная гипотеза — предположение, что P принадлежит целому классу распределений. Как правило, исследователь проверяет простую гипотезу.
Эта исходная гипотеза обычно называется нулевой. Что может выступить в таком качестве? В определенном смысле — что угодно, любое утверждение об исследуемой системе. Например, если у нас есть данные о росте призывников, мы можем проверить гипотезу, что неизвестный средний рост равен 1,76 м (или 2,10 м). Если у нас есть данные по количеству аистов и новорожденных, то мы можем проверить гипотезу, что эти две величины независимы. Если у нас есть два больших литературных произведения, мы можем проверять гипотезу, что их написал один автор, построив какую-то математическую модель.
Классическая постановка вопроса при этом такова: позволяют ли наблюдения отвергнуть нулевую гипотезу или нет? Точнее, с какой долей уверенности мы можем утверждать, что наблюдения нельзя получить, исходя из нулевой гипотезы? При этом, если мы не смогли доказать, опираясь на статистические данные, что нулевая гипотеза ложна, то она принимается истинной.
Тут можно подумать, что исследователи вынуждены совершать одну из классических логических ошибок, которая носит звучное латинское имя ad ignorantiam. Это аргументация истинности некоторого утверждения, основанная на отсутствии доказательства его ложности. Классический пример — слова, сказанные сенатором Джозефом Маккарти, когда его попросили предъявить факты для поддержки выдвинутого им обвинения, что некий человек — коммунист: «У меня немного информации по этому вопросу, за исключением того общего заявления компетентных органов, что в его досье нет ничего, что бы исключало его связи с коммунистами». Или еще ярче: «Снежный человек существует, поскольку никто не доказал обратного». Выявление разницы между научной гипотезой и подобными уловками составляет предмет целой области философии: методологии научного познания. Один из ее ярких результатов — критерий фальсифицируемости, выдвинутый замечательным философом Карлом Поппером в первой половине XX века. Он призван отделять научное знание от ненаучного и на первый взгляд кажется парадоксальным:
Теория или гипотеза может считаться научной, только если существует, пусть даже гипотетически, способ ее опровергнуть.
Чем не один из законов мерфологии? Получается, любая научная теория автоматически потенциально неверна, а теория, верная «по определению», не может считаться научной5.
Но всё же: почему, если мы не можем на базе статистических данных отвергнуть гипотезу, мы вправе считать ее истинной? Дело в том, что статистическая гипотеза берется не из желания исследователя или его предпочтений, она должна вытекать из каких-то общих формальных законов.
Например, из центральной предельной теоремы либо принципа максимальной энтропии, о котором мы поговорим в самом конце книги. Эти законы корректно отражают степень нашего незнания, не добавляя без необходимости лишних предположений или гипотез. В известном смысле это прямое использование знаменитого философского принципа, известного как бритва Оккама:
Что может быть сделано на основе меньшего числа предположений, не следует делать, исходя из большего.
Вообще с точки зрения принципа фальсифицируемости любое утверждение о существовании чего-либо ненаучно, ведь отсутствие свидетельства ничего не доказывает. В то же время утверждение об отсутствии чего-либо можно легко опровергнуть, предоставив экземпляр, косвенное свидетельство или доказав существование по построению. И в этом смысле статистическая проверка гипотез анализирует утверждения об отсутствии искомого эффекта и может предоставить в известном смысле точное опровержение.
Именно этим в полной мере оправдывается термин «нулевая гипотеза»: она содержит необходимый минимум знаний о системе.
1. Надо признаться, что эта фраза, ставшая расхожей с легкой руки Марка Твена, не была произнесена Дизраэли, и вообще неясно, кто ее автор.
2. Earl N., Simmonds I., N. Tapper N. Weekly cycles in peak time temperatures and urban heat island intensity // Environ. Res. Lett . 2016. Vol. 11.
3. Bäumer D., Vogel B. An unexpected patt ern of distinct weekly periodicities in climatological variables in Germany // Geophysical Research Lett ers. 2007. Vol. 34.
4. Издана на русском языке: Браст С. Исола. — М.: АСТ, 2002.
5. Более того, критерию Поппера не удовлетворяют такие науки, как математика и логика; впрочем, их относят не к естественным наукам, а к формальным. Однако очень важно понимать, что принцип фальсифицируемости говорит не об истинности теории, а только о том, научна она или нет. Он помогает определить, дает ли некая теория язык, на котором имеет смысл рассуждать о мире, или нет.


