6 марта в рамках проекта «Публичные лекции "Полит.ру"» выступил Александр Ханиевич Шень – кандидат физико-математических наук, старший научный сотрудник Лаборатории теории передачи информации и управления ИППИ РАН, научный сотрудник LIRMM CNRS (Франция, Монпелье). Тема его лекции «Основания теории вероятностей и колмогоровская сложность».
В «Демографическом энциклопедическом словаре» 1985 года издания в качестве примера возрастно-половой пирамиды приводится пирамида населения Мексики на январь 1970 года. На первый взгляд в ней не было ничего необычного. По вертикальной оси отмечается возраст, по горизонтальной – количество людей, слева – мужчины, справа – женщины. Длина полосок соответствует числу лиц этого возраста.
Но, присмотревшись, можно заметить странное явление. Начиная с возраста 30 лет и далее для возрастов 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85 лет мы видим, что количество людей значительно превышает число тех, чей возраст не кратен пяти. Что это? В Мексике раз в пять лет старались больше рожать? Или люди, рожденные в эти годы, обладают повышенной выживаемостью? Специалистам по демографии ответ на этот вопрос известен. Просто люди, многие из которых не были очень грамотны, на вопрос переписчика о возрасте называли округленное число. Поскольку перепись населения регистрирует все данные не по документам, а со слов опрашиваемых, итоговые данные приняли такой вид.
Здесь неожиданно обнаруженная закономерность заставила нас усомниться в верности исходных данных. А что бывает, когда мы смотрим на последовательности, полученные в результате случайных процессов? Мы бросаем монету и получаем такую последовательность (0 – орел, 1 – решка):
11011100111011111010011001101011100000111101.
Или мы бросаем шестигранную кость и получаем последовательность, например, такую:
44215665323414612456423363165524112145645692.
Вроде, ничего подозрений не вызывает. А теперь представим, что результаты бросания монеты или кости оказались иными и последовательности выглядят так:
11111111111111111111111111111111111111111111.
Или так:
100100100100100100100100100100100100100100100.
Или так:
123456123456123456123456123456123456123456123456.
Мы сразу начинаем подозревать, здесь что-то неладное. Мы удивлены, также, как удивлены были главные герои пьесы Стоппарда «Розенкранц и Гильденстерн мертвы», когда монета более восьмидесяти раз упала орлом вверх. Мы предполагаем обман, неправильную монету или какое-то еще вмешательство. Полученные результаты кажутся нам маловероятными.
Между тем, они ничуть не менее вероятны, чем любые другие. Последовательное выпадение одних орлов имеет такую же вероятность, как и любой другой набор орлов и решек. Ведь итог каждого испытания не зависит от итогов предыдущих. И выпадение пяти решек подряд ничуть не увеличивает вероятность выпадения орла в шестой попытке.
Кстати, этот принцип независимости результата от предыдущих испытаний часто противоречит интуиции человека, а порой с гневом им отвергается. Александр Шень привел цитату из рассказа Эдгара Аллана По «Тайна Мари Роже», в котором автор с видом знатока теории вероятностей утверждает прямо противоположное:
«Это одна из тех аномалий, которые, хотя и чаруют умы, далекие от математики, тем не менее полностью постижимы только для математиков. Например, обычного читателя почти невозможно убедить, что при игре в кости двукратное выпадение шестерки делает почти невероятным выпадение ее в третий раз и дает все основания поставить против этого любую сумму. Заурядный интеллект не может этого воспринять, он не может усмотреть, каким образом два броска, принадлежащие уже прошлому, могут повлиять на бросок, существующий еще пока только в будущем. Возможность выпадения шестерки кажется точно такой же, как и в любом случае – то есть зависящей только от того, как именно будет брошена кость. И это представляется настолько очевидным, что всякое возражение обычно встречается насмешливой улыбкой, а отнюдь не выслушивается с почтительным вниманием. Суть скрытой тут ошибки – грубейшей ошибки – я не могу объяснить в пределах места, предоставленного мне здесь, а людям, искушенным в философии, никакого объяснения и не потребуется. Тут достаточно будет сказать, что она принадлежит к бесконечному ряду ошибок, которые возникают на пути Разума из-за его склонности искать истины в частностях».
И все же, чем отличаются последовательности, вызвавшие у нас сомнение, от других? В этих последовательностях распределение результатов подчиняется некоторой закономерности, которая позволяет описать эту последовательность, причем описание будет короче самой последовательности.
Последовательность:
11111111111111111111111111111111111111111111.
Описание:
44 единицы
Последовательность:
100100100100100100100100100100100100100100100.
Описание:
100, повторить 15 раз
Последовательность:
123456123456123456123456123456123456123456123456.
Описание:
Натуральные числа от 1 до 6, повторить 8 раз.
Анализируя подобные последовательности, известный математик Андрей Николаевич Колмогоров сформулировал понятие, которое впоследствии получило название колмогоровская сложность. Сложность последовательности – это минимальная длина программы, которая порождает данную последовательность. У последовательности из 44 единиц подряд колмогоровская сложность невелика, а вот у самой первой из приведенных нами последовательностей – напротив, сложность большая. Гораздо меньше места займет запись последовательности, чем описание алгоритма ее порождения.
В лекции Александр Шень сообщил малоизвестные подробности из истории понятия сложности. Независимо от Колмогорова примерно в то же время к формулировке такого понятия пришли еще два математика. Это Грегори Чайтин (Gregory Chaitin), который написал свою первую статью на эту тему, еще будучи школьником. И еще один американский математик Рэй Соломонофф (Ray Solomonoff).
Где понятие сложности может встретиться в жизни простого человека? При работе компьютера порой используют программы-архиваторы, которые сжимают размер файла, чтобы тот занимал меньше места на диске. Сжатие файлов основано, грубо говоря, на том, что программа находит закономерности в размещении кулей и единиц в его двоичной записи. Файл, колмогоровская сложность которого мала, сжимается хорошо, в несколько раз. Размер файла, колмогоровская сложность которого велика, при архивировании сильно не уменьшится. Фактически размер сжатого файла – это верхняя оценка его колмогоровской сложности (остается некоторый шанс, что закономерность есть, но программа-архиватор ее не нашла).
Приложениями колмогоровской сложности для классификаций занимается современный нидерландский математик Пол Витаньи (Paul Vitanyi). В одной из работ он сделал попытку построение классификации некоторого набора музыкальных произведений на основе сжатия midi-файлов с ними. При этом файлы х и у считались близкими, если сложность файла ху была меньше суммы сложностей файлов х и у. В результате, как оказалось, близкими по этой классификации оказались музыкальные произведения, действительно принадлежащие одному автору.
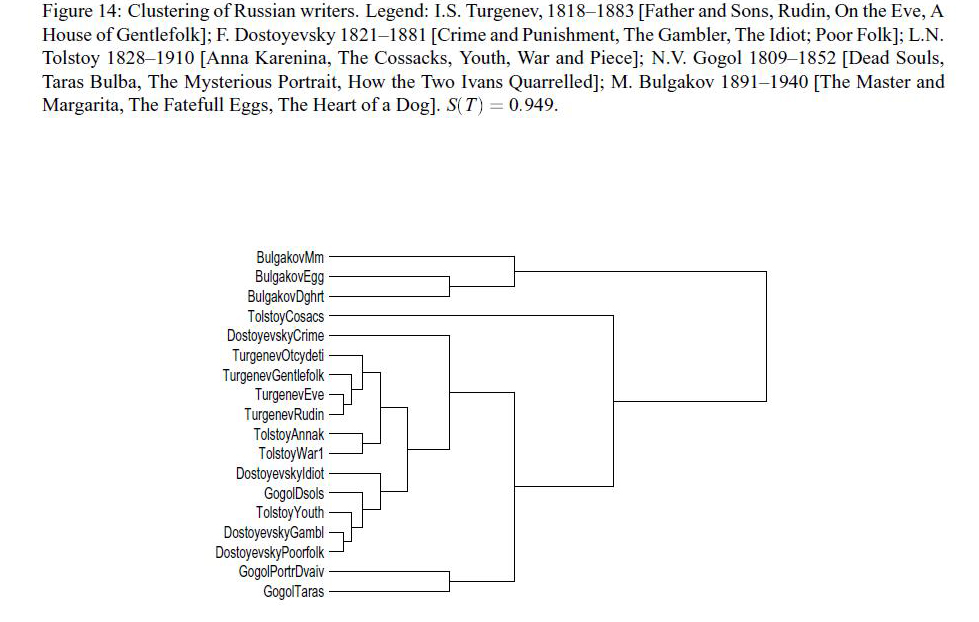
Также Полу Витаньи принадлежать попытки классификаций по сжатию текстов произведений русской литературы классиков и их переводов.
В других случаях им и его соавторами этот метод использовался для определения места вируса тяжелого острого респираторного синдрома (SARS) среди других вирусов по последовательности нуклеотидов в его РНК, классификации видов млекопитающих по ДНК, грибов по митохондриальным ДНК и даже построения классификации языков по текстам декларации прав человека, переведенным на эти языки. Подробнее об этом можно прочитать в работах The similarity metric (pdf) и Clustering by compression (pdf).